I'm Popular!!
In the alternate universe of my dreams, I get to answer questions about probability! Wow! I’m beyond flattered. At first there are only two people, but soon more people start to join. I’ll wake up happy if I can finish answering each of their questions. What’s the expected amount of time until there are \(n\) people in line?
Let’s first deal with the slightly more realistic situation where there are 2 people who want to ask me a question. Since we are looking for the time until I finish answering we can model this as an exponential distribution - let’s say I can answer questions with an average time of 8 minutes each, rate 0.125. Then there are only two possible situations, either I finish the first person’s question before the 2nd person arrives or I take longer and the second person has to wait before I get to her. Let’s say that the second person arrives 5 minutes after the first person arrives. Thus how can I compute the expected time conditioned on the fact that I know the second person arrives 5 minutes after the first?
Let’s write out the expected value for the first case. Once again the total expectation of an event occurring can be written as the sum of the probability each possible event occurs multiplied by the value generated by that event.
\[X = \text{random var for time spent answering questions}\]How do we compute the probability that I took less than 5 minutes to answer the first question? This is a simple Cumulative density function (CDF) or an integration of the probability density function from 0 to 5. If we were to compute out this integral again, we’d find that the CDF of an exponential random variable is \(1 - e^{-\lambda x}\). The expected value of an exponential random variable is \(\frac{1}{\lambda}\) as derived previously. Thus we have both parts of this equation.
Now for the second scenario, we know that it takes me more than 5 minutes to answer the first question making the second person wait. But given this, how do we figure out how much additional time is needed?
\[E[X] = P(X_1 > 5) \cdot (E(X_1 | X_1 > 5) + E[X_2])\]We have to condition on the fact that we know the first person took more than 5 minutes in order to find the total time spent. Why? Given that you know she didn’t answer the question in the first let’s say even 60 minutes, is it now more likely that she’ll finish answering quickly versus if there wasn’t this delay?
The Memoryless Property
Ok so we need to compute \(E(X_1 \mid X_1 > 5)\). Let’s first look at \(P(X > s + t \mid X > s)\). Let’s expand this conditional probability out and then simplify the expression.
\[\begin{align} P(X > s + t | X > s) &= \frac{P(X > s+t \text{ and } X > t)}{P(X > s)} \\ &= \frac{P(X > s+t)}{P(X > s)}\\ &= \frac{e^{-\lambda(s+t)}}{e^{-\lambda s}}\\ &= e^{-\lambda t} \end{align}\]We know that if \(X > s+t\) then X is guaranteed to be greater than t. Thus we can simplify the numerator in the second step. Then we have a fraction of two CDFs. We compute the CDF functions and cancel terms, leaving us without any information regarding the time delay. This literally states that regardless of the past, the expected future time will remain the same - its the memoryless property of the exponential function.
Therefore \(E[X_1 \mid X_1 > 5] = 5 + E[X_1]\). We can thus write out the entire expression now.
\[\begin{align} E[X] &= P(X_1 < 5) \cdot (5 + E[X_2]) + P(X_1 > 5) \cdot (E(X_1 | X_1 > 5) + E[X_2])\\ &= (1 - e^{-.125x})(5 + 5) + (1 - (1- e^{-.125x}))(5 + 5 + 5)\\ &= (1 - e^{-.125(5)}(10) + (e^{-.125(5)})(15))\\ &= 13.38 \end{align}\]Great I get to be in the limelight for a little over 13 minutes!
A Queue of People
My dream whirls on and now there’s an entire line of people! If a new person joins the line every 12 minutes, how long can I expect it to take before there are \(n\) people in the queue?
Thus here we have two situations happening simultaneously. On one end I am answering questions at a rate of 1 every 8 minutes. On the other end, new people are joining the line to have questions at a rate of 1 every 12 minutes. Given the fact that I can answer questions faster than people join, it looks promising that I’ll be able to answer every question. To better understand the situation, let’s try drawing it out as a Continuous Time Markov Chain. We can let \(\lambda\) represent the rate of people joining the queue and \(\mu\) represent the rate of people leaving the queue with a solution.
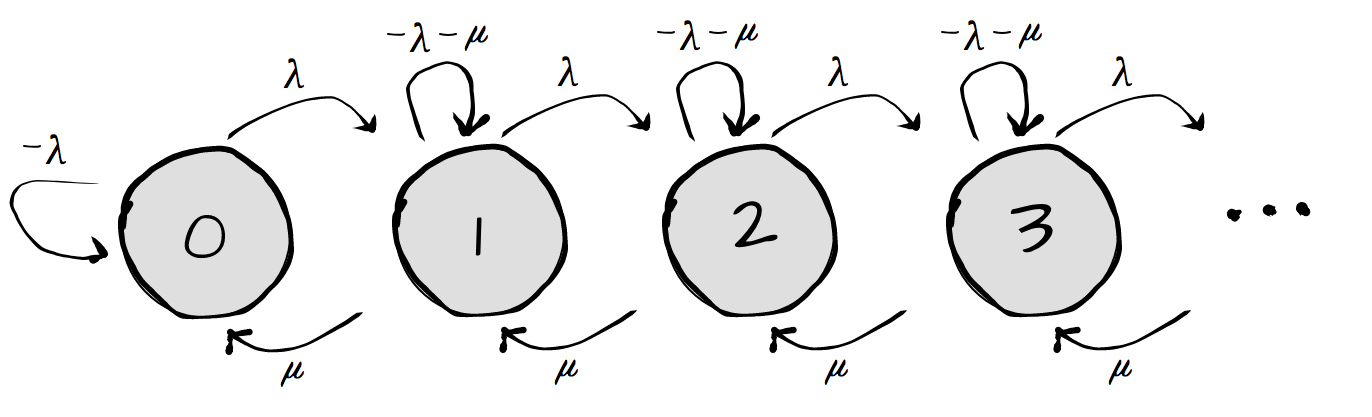
Now if we go back to the discrete time case, we wrote out the following equation
\[\pi_{n+1} = \pi_{n} P\]This stated that the probability distribution among states in time \(n+1\) was equal to the probability distribution in time \(n\) times the transition matrix. In the continuous time case we don’t have discrete intervals and thus we took the limit as this time interval becomes infinitely small. Thus instead of \(\pi_{n+1}\) we have the derivative of the change in the probability distribution represented as \(\frac{dP(t)}{dt}\) where \(P(t)\) is the change in the probability distribution. The transition matrix is also changed to represent the transitions as the time interval goes to 0 \(Q\). Thus for the continuous case we have
\[\frac{dP(t)}{dt} = P(t) Q\]Great. What is our matrix \(Q\) here?
The self transition probabilities must be \(-\lambda - \mu\) because in order for this to be a valid transition matrix the probability of transitioning out of a node must equal the probability of transitioning into the node.
Given Infinite Time..
Now how do we compute the stationary distribution in each state and then the expected time to reach state n?
Once again let’s start by going back to the stationary case. Here we said that in order to find the expected time to reach a given state we can first find the long term expected time spent in each state. Once we know this long run distribution we can then compute the expected time to reach the state as the fraction of time spent in this state.
Will this Markov Chain have a stationary distribution? Yes - all the states are recurrent (for every state once you leave, you have a finite probability of returning to it in a finite amount of time) and aperiodic (there aren’t cycles). We can write out the equation for the stationary distribution as
This states that the change in the probability distribution is 0 and thus it is stationary.
\[\begin{bmatrix} \pi_0 & \pi_1 & \pi_2 & \pi_3 & ... \end{bmatrix} \begin{bmatrix} -\lambda & \lambda & 0 & 0 & ...\\ \mu & -\lambda - \mu & \lambda & 0 & ...\\ 0 & \mu & -\lambda - \mu & \lambda & ... \\ 0 & 0 & \mu & . &... \\ . & . & . & . & ... \end{bmatrix} = \begin{bmatrix} 0 & 0 & 0 & 0 & ... \end{bmatrix}\] \[\begin{align} -\lambda \pi_0 + \mu \pi_1 &= 0\\ \lambda \pi_0 + (-\mu -\lambda) \pi_1 + \mu \pi_2 &= 0\\ \lambda \pi_1 + (-\mu -\lambda) \pi_2 + \mu \pi_3 &= 0\\ \pi_1 = \frac{\lambda}{\mu} \pi_0\\ \pi_2 = \frac{\lambda}{\mu} ^ 2 \pi_0\\ \pi_n = \frac{\lambda}{\mu} ^ n \pi_0\\ \end{align}\]With the normalization equation
\[\pi_0 \sum_{n=0}^{\infty} \frac{\lambda}{\mu}^n = 1\]Here we can use the equation for the infinite geometric series
\[\pi_0 = 1 - \frac{\lambda}{\mu}\]Thus combining the equation derived through recurrence for \(\pi_n\) in terms of \(\pi_0\), the probability of having \(n\) people in the queue is
\[\pi_n = (\frac{\lambda}{\mu})^n (1 - \frac{\lambda}{\mu})\]Many Many Questions!
Now we can find the amount of time until there are \(n = 10\) people in line. We found the stationary distribution of the queue of people thus we know that the expected time until reaching that state can be computed as the inverse of the stationary distribution. For the case of computing the time until there are 10 people in line, an arrival rate of \(\frac{1}{12}\) and a departure rate of \(\frac{1}{8}\), we have the following
\[\pi_{10} = (\frac{.083}{.125})^{10} - (1-\frac{.083}{.125}) = 0.0056\]Thus \(\frac{1}{.0056} = 178 = 2.9 \text{hours}\)
In about 3 hours there are 10 people in line. Hopefully these people don’t run away disappointed :P