Where lunch?
People arrive independently and at random times to work in the research lab. From observation, I’ve come to expect that \(\lambda\) people arrive there to work per hour. On a given day, everyone there decides to get lunch at one of the \(m\) restaurants nearby. We can’t unanimously decide on a place to eat so we each choose where to eat independently. If each of us has an equal probability of going to each restaurant, can we figure out the expected number of different restaurants we cover as a group?
Ok first the expected number of restaurants visited will naturally depend on the number of people that go to get food. All we know is that during a given hour, I expect \(\lambda\) people to arrive and that they arrive independently and randomly. Given this, at any given instant can I compute the probability that \(k\) people have arrived?
Once I know the probability that there are a certain number, \(k\) people going to get food I then need to determine the expected number of restaurants they visit. Now each of these \(n\) people individually choose the restaurant they want to eat at with equal probability. If two people choose the same place, the expected number of places they visit remains the same. Given that the group splits off to get food from their desired location, how can we compute the expected number of restaurants they visit?
The Poisson
Let’s start by tackling the first question. We need a way to compute the probability that at a given moment of time there are \(n\) people present and they arrive at a rate of \(\lambda\) per hour. How can we model this? We can first think of drawing this out as a graph. Each state represents the number of people in lab. Let’s make the assumption that once a person arrives, he or she doesn’t leave until after lunch. Also once again we don’t have discrete transition probabilities; instead we have the probability of transitioning as a function of time.
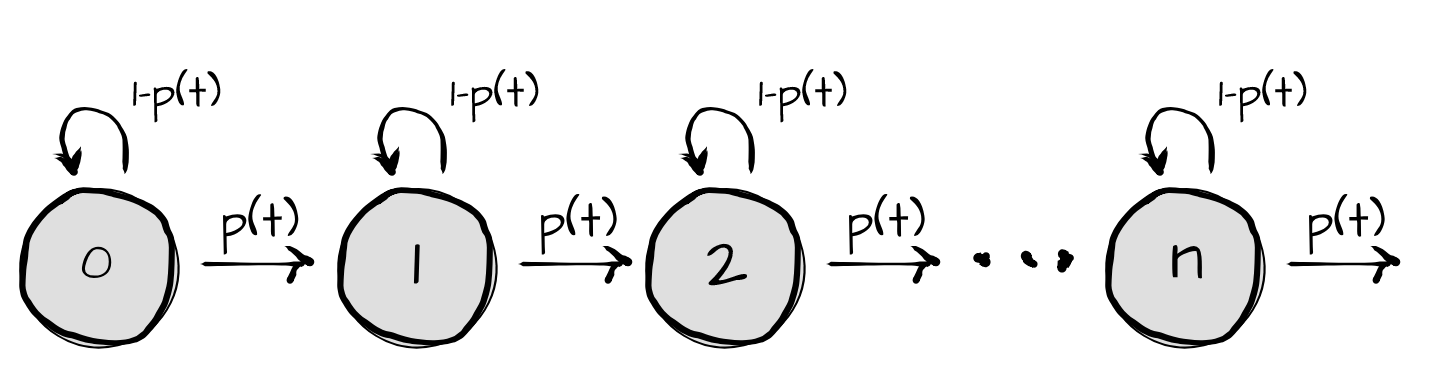
As with the derivation of the exponential function, we can continue on to compute the derivative of these transition functions to figure out the probability of transitioning as the time interval \(\delta t\) becomes infinitely small.
To avoid hairy matrix derivatives though, can we think of another way of computing the probability as the time interval becomes increasingly small?
Poisson Distribution and the Binomial Distribution
We know that we expect \(\lambda\) people to arrive every hour. What if we divide this into smaller time increments and compute the probability of some number of arrivals in that interval?
\[E[X] = \frac{\lambda}{60 mins} \cdot \frac{60 mins}{hour}\]The first term \(\frac{\lambda}{60 mins}\) represents the rate or probability of arrival per minute while \(\frac{60 mins}{hour}\) is the number of intervals.
Given this probability of arrival per minute we can compute \(P(X=x)\) using the binomial distribution!
This isn’t completely accurate though because you are counting a success if a person arrives in a given minute. However you might have 2 people arriving within the same minute and they wouldn’t be distinguished or reflected in the count k. Thus we can continue to make smaller and smaller time intervals. If we take the limit as the time interval goes to infinity we have the following
\[P(X = k) = \lim_{n \to \infty } \binom{n}{k} (\frac{\lambda }{n})^k (1-\frac{\lambda }{n})^{(n-k)}\]In order to compute this limit we know this holds from calculus:
\[e = \lim_{n \to \infty } (1 + \frac{1}{n})^n\]We can now simplify the limit:
\[P(X=k) = \lim_{n \to \infty } \left ( \frac{n!}{(n-k)! k!} \right ) \left ( \frac{\lambda}{n} \right )^k \left ( 1- \frac{\lambda}{n} \right )^n \left ( 1- \frac{\lambda}{n} \right )^{(-k)}\]We pull out terms that don’t depend on n
\[P(X=k) = \left ( \frac{\lambda^k}{k!} \right )\lim_{n \to \infty } \left ( 1 - \frac{\lambda}{n} \right )^n \left ( 1- \frac{\lambda}{n} \right )^{(-k)}\]We know that since k is a constant the last term will go to 0 and thus we have
\[P(X=k) = \left ( \frac{\lambda^k}{k!} \right )\lim_{n \to \infty } \left ( 1 - \frac{\lambda}{n} \right )^n\]Here by the definition of e we have the formula for a Poisson random variable
\[P(X=k) = \left ( \frac{\lambda^k}{k!} \right ) e^{-\lambda}\]Essentially all we have done here is to break up our rate into increasingly smaller time segments. Then taking the limit as these time intervals go to infinity we can now compute the probability of any number of intervals in the given time period.
Poisson Splitting
Now given that we have modeled the arrivals of people as a Poisson process, how can we compute the expected number of places they go to?
Essentially you want to split the Poisson process into multiple different Poisson processes, one for each of the n restaurants they can go to.
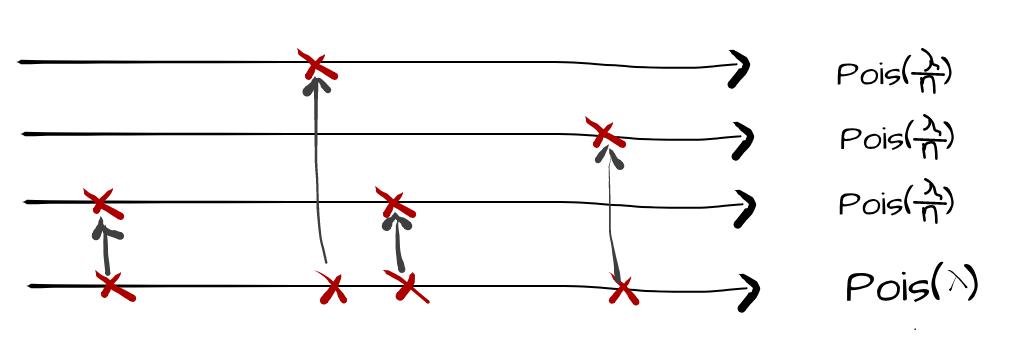
Since people choose where to eat with the same probability, you now have \(Pois(\frac{\lambda}{n})\). We know these are also Poisson because they follow the random exponentially distributed arrival times. Now the problem lies in determining the number of unique restaurants visited. We can model this using the indicator variable \(Y\).
\[Y = \left\{\begin{matrix} 1 \text{ at least 1 visit}\\ 0 \text{ otherwise} \end{matrix}\right.\]Now we need to use this to determine the probability that at least one person chooses a particular restaurant. In other words how do we find the probability of one arrival in a Poisson process?
\[P(X \geq 1) = 1 - P(X = 0)\]We can directly substitute in 0 for \(x\) in order to get
\[1 - P(X=0) = (1 - e^{\frac{-\lambda}{n}})\]Since each restaurant is equally likely this results in the following expectation
\[E[Y] = n(1-e^{\frac{-\lambda}{n}})\]Thus we have determined the expected number of restaurants that will be visited! Let’s quickly put in the actual numbers. I estimate that people arrive at a rate of 4 people per hour and there are 8 restaurants on the street nearby. Thus we have
\[E[Y] = 8(1-e^{\frac{-4}{8}}))\] \[E[Y] = 3.14\]We can expect to go to around \(\pi\) different restaurants!