I love listening to music while I work, but often times I find myself listening to the same songs over and over again. If I replace my playlist with some probability every day, how many days can I expect my playlist to last?



We can start by thinking about this intuitively. What’s the probability of replacing my playlist after 3 days? Well this would be the probability of the following sequence of events. Here \(p_{i,j}\) represents the probability of transitioning from state \(i\) to state \(j\).

\[P(X=3) = p_{0,1} \cdot p_{1,2} \cdot p_{2,3} \cdot p_{3,0}\]

Plugging in our values this gives us

\[P(X=3) = 0.92 \cdot 0.92 \cdot 0.92 \cdot 0.08\] \[P(X=3) = 0.062\]

Thus I have a 6.2% chance of replacing my playlist after 3 days. We can do this for any desired sequence of events that we want to find. The main reason we can compute this probability is that given that the playlist has existed for 5 days knowing anything about what happened on previous days doesn’t give us any more information. Thus it satisfies the Markov property - the probability of future states conditioned on the present and past states, depends only on the present state not the sequence of states before it. Thus we could try computing this out for each such number of days and then manually figure out the expected number of days. However this quickly becomes infeasible for any large number of states.

Let’s first represent this as a graph. Here each node represents the number of days that the playlist has lasted before being replaced.


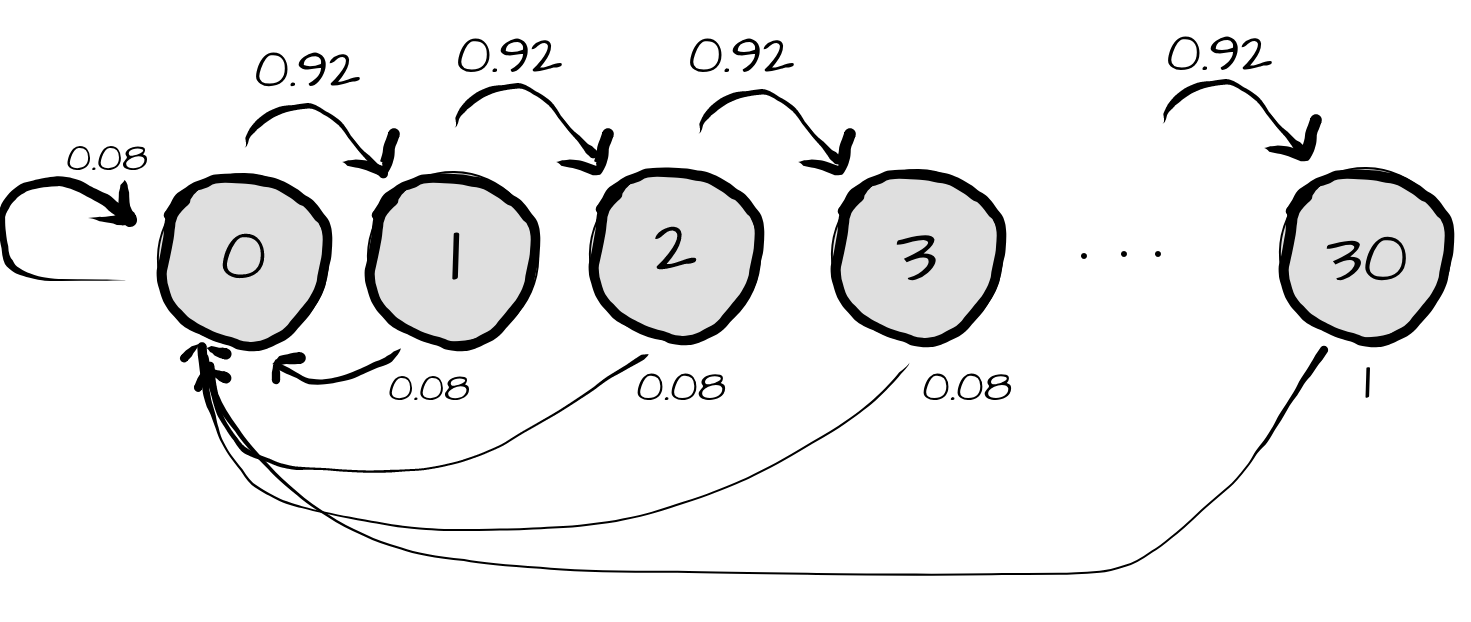
Markov Chain

Now we can think of running a simulation allowing a particle to travel along this graph moving according to the transition probabilities and record the number of times it lands in each state. As \(n \to \infty\) we have a good estimate of how many times each state is visited. This represents the long term fraction of time spent in each state.

We can take that intuition and derive an analytic solution. Let’s write out all the transition probabilities in matrix form

\[\pi_{n+1} = \pi_{n} \begin{bmatrix} 0.08 & 0.92 & 0 & ... \\ 0.08 & 0 & 0.92 & ... \\ 0.08 & 0 & 0 & ...\\ . & . & . & \end{bmatrix}\]

Here \(\pi\) represents the distribution over the current states. Thus after multiplying by the transition matrix you get the distribution for the next time step. Now we want to find the distribution when the number of time steps goes to infinity. In this case as n goes to infinity this distribution converges to a stationary distribution, however this isn’t always the case.

As this \(30x30\) matrix is very tedious to work with, we can instead use a more sparse representation of the transitions. Here we will let \(p\) represent the probability of keeping the playlist and \(1-p\) represent the probability of replacing it.

\[\begin{align} \pi_0 &= p\pi_1 + p\pi_2 + p\pi_3 + ... + p\pi_{30}\\ \pi_1 &= (1-p)\pi_0\\ \pi_2 &= (1-p)\pi_1\\ &= (1-p)(1-p)\pi_0\\ ...\\ \pi_i &= (1-p)^i\pi_0\\ \end{align}\]

These equations essentially are an expanded form of the above matrix multiplication. Now we can solve for \(\pi_0\). In order to do this we need one more equation - we can use the fact that the sum of the fractions in each state must equal 1. Then we go ahead and substitute in the formula derived for \(\pi(i)\) in terms of \(\pi(0)\).

\[\begin{align} 1 &= \pi_0 + \sum_{i=1}^{30}\pi_i \\ 1 &= \pi_0 + \sum_{i=1}^{30}(1-p)^i\pi_0 \\ 1 &= \pi_0 (1 + \sum_{i=1}^{30} (1-p)^i) \end{align}\]

We want to solve this equation for \(\pi_0\). We note that we have a finite geometric sum and thus can use the following formula for the sum of a finite geometric series:

\[\sum_{i=0}^{n} x^i = \frac{1 - x^{n+1}}{1-x}\]

Thus we have

\[\pi_0 = \frac{p}{1 - (1-p)^{31}}\]

Substituting in the actual value for \(p\) we have

\[\begin{align} \pi_0 &= \frac{0.08}{1 - (0.92)^{31}} \\ &= 0.086 \end{align}\]

Thus we now know the long term fraction of time spent in state 0. How can we use this to compute the expected number of days until I replace my playlist? How does knowing the long term fraction of time spent in this state help solve that?

Well intuitively we can go back to the simulation we started off with. There we counted the long term fraction of time in a state as the number of visits to a state over the total number of time steps. Essentially that’s how long you spend in that state compared to the others. Now if we were to have a two state Markov chain and had a long term fraction of time spent in each state as \(\frac{1}{2}\), the expected time to reach one of the states would intuitively be 2. The same holds for 3 states - essentially you visit the state once for every 3 states you visit. Thus the expected time can be computed as the reciprocal of the long term fraction of time spent in that state. This gives us \(1/0.086\) or an expected time of 11.6 days before I replace my entire music playlist. Neat!